

The period of a mass attached to a pendulum of length ℓ with gravitational acceleration g is given by In the small-angle approximation, the motion of a simple pendulum is approximated by simple harmonic motion. The motion of an undamped Pendulum approximates to simple harmonic motion if the amplitude is very small relative to the length of the rod. The total mechanical energy of the system therefore has the constant value Examples The kinetic energy K of the system at time t is These equations demonstrate that the simple harmonic motion is isochronous (the period and frequency are independent of the amplitude and the initial phase of the motion).

Using the techniques of differential calculus, the velocity and acceleration as a function of time can be found:Īcceleration can also be expressed as a function of displacement:Īnd since T = 1/ f where T is the time period, Each of these constants carries a physical meaning of the motion: A is the amplitude (maximum displacement from the equilibrium position), ω = 2π f is the angular frequency, and φ is the phase. In the solution, c 1 and c 2 are two constants determined by the initial conditions, and the origin is set to be the equilibrium position. Solving the differential equation above, a solution which is a sinusoidal function is obtained.
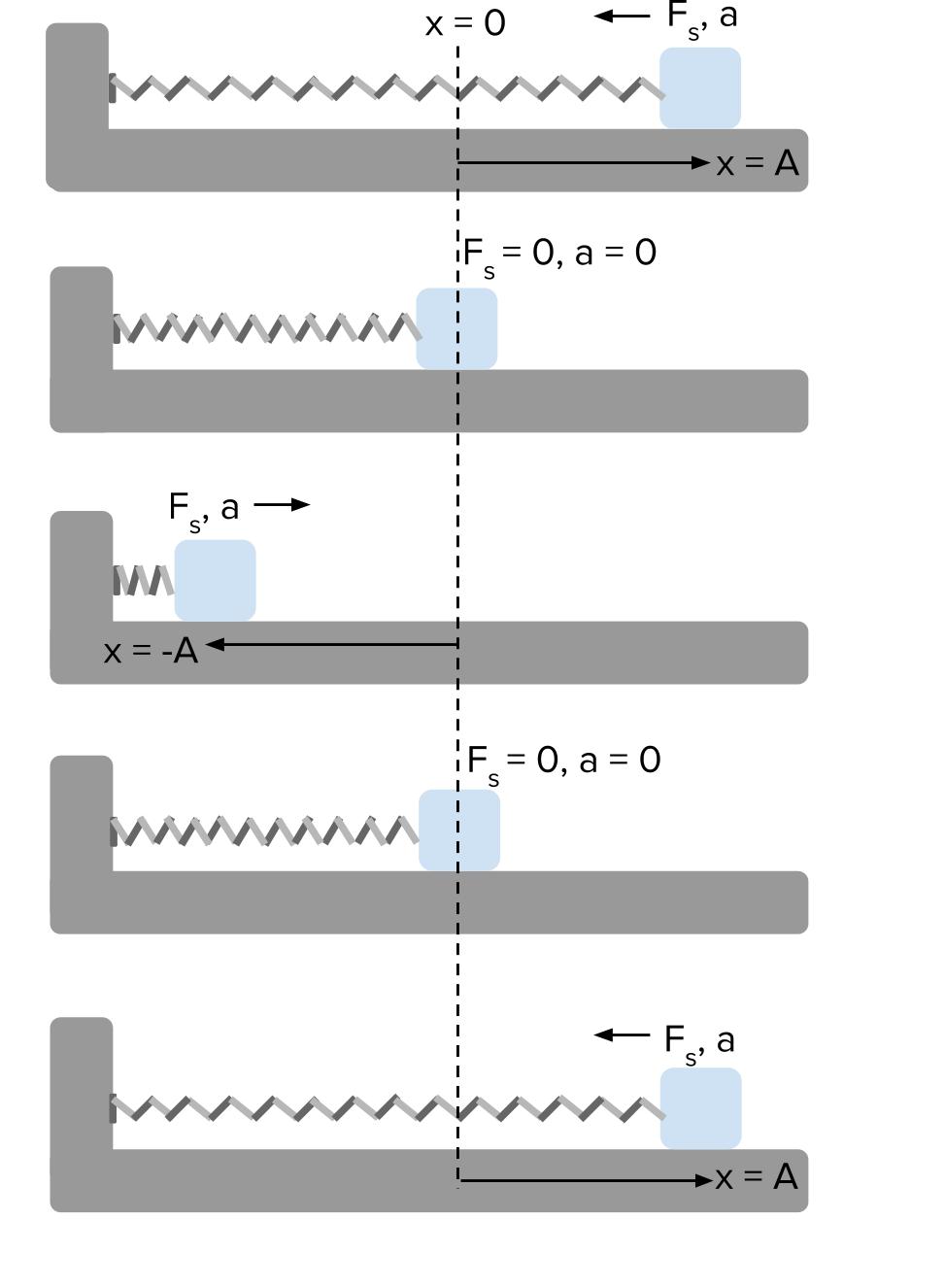
Where m is the inertial mass of the oscillating body, x is its displacement from the equilibrium (or mean) position, and k is the spring constant. Dynamics of simple harmonic motionįor one-dimensional simple harmonic motion, the equation of motion, which is a second-order linear ordinary differential equation with constant coefficients, could be obtained by means of Newton's second law and Hooke's law. Thus, simple harmonic motion is a type of periodic motion. A net restoring force then tends to slow it down, until its velocity vanishes, whereby it will attempt to reach equilibrium position again.Īs long as the system has no energy loss, the mass will continue to oscillate. Therefore, the mass continues past the equilibrium position, compressing the spring. However, at x = 0, the mass has momentum because of the impulse that the restoring force has imparted. At the equilibrium position, the net restoring force vanishes. When the mass moves closer to the equilibrium position, the restoring force decreases. As a result, it accelerates and starts going back to the equilibrium position. Once the mass is displaced from its equilibrium position, it experiences a net restoring force. When the system is displaced from its equilibrium position, a restoring force which resembles Hooke's law tends to restore the system to equilibrium.m −1), and x is the displacement from the equilibrium position (in m).Where F is the restoring elastic force exerted by the spring (in SI units: N), k is the spring constant ( N Mathematically, the restoring force F is given by However, if the mass is displaced from the equilibrium position, a restoring elastic force which obeys Hooke's law is exerted by the spring. If the system is left at rest at the equilibrium position then there is no net force acting on the mass. (Here the velocity and position axes have been reversed from the standard convention in order to align the two diagrams)Ī simple harmonic oscillator is attached to the spring, and the other end of the spring is connected to a rigid support such as a wall. Simple harmonic motion shown both in real space and phase space.


 0 kommentar(er)
0 kommentar(er)
